Nested Loops Joins and Performance Spools

Introduction
Performance spools are lazy spools added by the optimizer to reduce the estimated cost of the inner side of nested loops joins. They come in three varieties: Lazy Table Spool, Lazy Index Spool, and Lazy Row Count Spool. An example plan shape showing a lazy table spool is below:
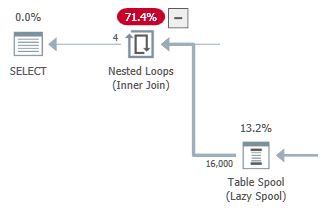
The questions I set out to answer in this article are why, how, and when the query optimizer introduces each type of performance spool.
Just before we get started, I want to stress an important point: There are two distinct types of nested loop join in execution plans. I will refer to the variety with outer references as an apply, and the type with a join predicate on the join operator itself as a nested loops join. To be clear, this difference is about execution plan operators, not T-SQL query syntax. For more details, please see my linked article.
Performance Spools
The picture below shows the performance spool execution plan operators as displayed in Plan Explorer (top row) and SSMS 18.2 (lower row):
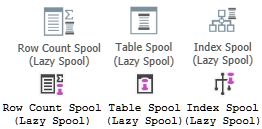
General remarks
All performance spools are lazy. The spool’s worktable is gradually populated, a row at a time, as rows stream through the spool. (Eager spools, by contrast, consume all input from their child operator before returning any rows to their parent).
Performance spools always appear on the inner side (the lower input in graphical execution plans) of a nested loops join or apply operator. The general idea is to cache and replay results, saving repeated executions of inner-side operators wherever possible.
When a spool is able to replay cached results, this is known as a rewind. When the spool has to execute its child operators to obtain correct data, a rebind occurs.
You may find it helpful to think of a spool rebind as a cache miss, and a rewind as a cache hit.
Lazy table spool
This type of performance spool can be used with both apply and nested loops join.
Apply
A rebind (cache miss) occurs whenever an outer reference value changes. A lazy table spool rebinds by truncating its worktable and fully repopulating it from its child operators.
A rewind (cache hit) occurs when the inner side executes with the same outer reference values as the immediately preceding loop iteration. A rewind replays cached results from the spool’s worktable, saving the cost of re-executing the plan operators below the spool.
Note: A lazy table spool only caches results for one set of apply outer reference values at a time.
Nested loops join
The lazy table spool is populated once during the first loop iteration. The spool rewinds its contents for each subsequent iteration of the join. With nested loops join, the inner side of the join is a static set of rows because the join predicate is on the join itself. The static inner-side row set can therefore be cached and reused multiple times via the spool. A nested loops join performance spool never rebinds.
Lazy row count spool
A row count spool is little more than a Table Spool with no columns. It caches the existence of a row, but projects no column data. Aside from noting its existence, and mentioning that it can be an indication of an error in the source query, I will not have more to say about row count spools.
From this point forward, whenever you see “table spool” in the text, please read it as “table (or row count) spool” because they are so similar.
Lazy index spool
The Lazy Index Spool operator is only available with apply.
The index spool maintains a worktable that is not truncated when outer reference values change. Instead, new data is added to the existing cache, indexed by the outer reference values. A lazy index spool differs from a lazy table spool in that it can replay results from any prior loop iteration, not just the most recent one.
The next step in understanding when performance spools appear in execution plans requires understanding a bit about how the optimizer works.
Optimizer Background
A source query is converted into a logical tree representation by parsing, algebrization, simplification, and normalization. When the resulting tree does not qualify for a trivial plan, the cost-based optimizer looks for logical alternatives that are guaranteed to produce the same results, but at a lower estimated cost.
Once the optimizer has generated potential alternatives, it implements each one using appropriate physical operators, and computes estimated costs. The final execution plan is built from the lowest cost option found for each operator group. You can read more details about the process in my Query Optimizer Deep Dive series.
The general conditions necessary for a performance spool to appear in the optimizer’s final plan are:
- The optimizer must explore a logical alternative that includes a logical spool in a generated substitute. This is more complex than it sounds, so I will unpack the details in the next main section.
- The logical spool must be implementable as a physical spool operator in the execution engine. For modern versions of SQL Server, this essentially means that all key columns in an index spool must be of a comparable type, no more than 900 bytes* in total, with 64 key columns or fewer.
- The best complete plan after cost-based optimization must include one of the spool alternatives. In other words, any cost-based choices made between spool and non-spool options must come out in favour of the spool.
* This value is hard-coded into SQL Server and has not been changed following the increase to 1700 bytes for nonclustered index keys from SQL Server 2016 onward. This is because the spool index is a clustered index, not a nonclustered index.
Optimizer Rules
We cannot specify a spool using T-SQL, so getting one in an execution plan means the optimizer has to choose to add it. As a first step, this means the optimizer has to include a logical spool in one of the alternatives it chooses to explore.
The optimizer does not exhaustively apply all the logical equivalence rules it knows to every query tree. This would be wasteful, given the optimizer’s goal of producing a reasonable plan quickly. There are multiple aspects to this. First, the optimizer proceeds in stages, with cheaper and more often applicable rules tried first. If a reasonable plan is found in an early stage, or the query does not qualify for later stages, optimization effort may terminate early with the lowest cost plan found so far. This strategy helps prevent spending more time on optimization than is saved by incremental cost improvements.
Rule matching
Each logical operator in the query tree is quickly checked for a pattern match against the rules available in the current optimization stage. For example, each rule will only match a subset of logical operators, and may also require specific properties to be in place, such as guaranteed sorted input. A rule may match to an individual logical operation (a single group) or a multiple contiguous groups (a subsection of the plan).
Once matched, a candidate rule is asked to generate a promise value. This is a number representing how likely the current rule is to produce a useful result, given the local context. For example, a rule might generate a higher promise value when the target has many duplicates on its input, a large estimated number of rows, guaranteed sorted input, or some other desirable property.
Once promising exploration rules have been identified, the optimizer sorts them into promise value order, and starts asking them to generate new logical substitutes. Each rule may generate one or more substitutes that will later be implemented using physical operators. As part of that process, an estimated cost is calculated.
The point of all this as it applies to performance spools is that the logical plan shape and properties must be conducive to matching spool-capable rules, and the local context must produce a high enough promise value that the optimizer chooses to generate substitutes using the rule.
Spool Rules
There are a number of rules that explore logical nested loops join or apply alternatives. Some of these rules can produce one or more substitutes with a particular type of performance spool. Other rules that match nested loops join or apply never generate a spool alternative.
For example, the rule ApplyToNL implements a logical apply as a physical loops join with outer references. This rule may generate several alternatives each time it runs. In addition to the physical join operator, each substitute may contain a lazy table spool, a lazy index spool, or no spool at all. The logical spool substitutes are later individually implemented and costed as the appropriately-typed physical spools, by another rule called BuildSpool.
As a second example, the rule JNtoIdxLookup implements a logical join as a physical apply, with an index seek immediately on the inner side. This rule never generates an alternative with a spool component. JNtoIdxLookup is evaluated early and returns a high promise value when it matches, so simple index-lookup plans are found quickly.
When the optimizer finds a low-cost alternative like this early on, more complex alternatives may be aggressively pruned out or skipped entirely. The reasoning is that it does not make sense to pursue options that are unlikely to improve on a low cost alternate already found. Equally, it is not worth exploring further if the current best complete plan has a low enough total cost already.
A third rule example: The rule JNtoNL is similar to ApplyToNL, but it only implements physical nested loop join, with either a lazy table spool, or no spool at all. This rule never generates an index spool because that type of spool requires an apply.
Spool Generation and Costing
A rule that is capable of generating a logical spool will not necessarily do so each time it is called upon. It would be wasteful to generate logical alternatives that have next to no chance of being chosen as cheapest. There is also a cost to generating new alternatives, which may in turn produce yet more alternatives—each of which may need implementation and costing.
To manage this, the optimizer implements common logic for all spool-capable rules to determine which type(s) of spool alternative to generate based on local plan conditions.
Nested loops join
For a nested loops join, the chance of getting a lazy table spool increases in line with:
- The estimated number of rows on the outer input of the join.
- The estimated cost of inner-side plan operators.
The cost of the spool is repaid by savings made avoiding inner-side operator executions. The savings increase with more inner iterations, and higher inner-side cost. This is especially true because the cost model assigns relatively low I/O and CPU cost numbers to table spool rewinds (cache hits). Remember that a table spool on a nested loops join only ever experiences rewinds, because the lack of parameters means the inner-side data set is static.
A spool may store data more densely than the operators that feed it. For example, a base table clustered index might store 100 rows per page on average. Say a query needs only a single integer column value from each wide clustered index row. Storing just the integer value in the spool worktable means well over 800 such rows can be stored per page. This is important because the optimizer assesses the cost of the table spool in part using an estimate of the number of worktable pages needed. Other costing factors include the per-row CPU cost involved in writing and reading the spool, over the estimated number of loop iterations.
The optimizer is arguably a little too keen to add lazy table spools to the inner side of a nested loops join. Nevertheless, the optimizer’s decision always makes sense in terms of estimated cost. I personally regard nested loops join as high risk, because they can quickly become slow if either join input cardinality estimate is too low.
A table spool may help reduce the cost, but it cannot fully hide the worst-case performance of a naive nested loops join. An indexed apply join is normally preferable, and more resilient to estimation errors. It is also a good idea to write queries that the optimizer can implement with hash or merge join when appropriate.
Apply lazy table spool
For an apply, the chances of getting a lazy table spool increase with the estimated number of duplicate join key values on the outer input of the apply. With more duplicates, there is a statistically higher chance of the spool rewinding its currently stored results on each iteration. An apply lazy table spool with a lower estimated cost stands a better chance of featuring in the final execution plan.
When the rows arriving on the apply outer input have no particular ordering, the optimizer makes a statistical assessment of how likely each iteration is to result in a cheap rewind or an expensive rebind. This assessment uses data from histogram steps when available, but even this best case scenario is more of an educated guess. Without a guarantee, the order of rows arriving on the apply outer input is unpredictable.
The same optimizer rules that generate logical spool alternatives may also specify that the apply operator requires sorted rows on its outer input. This maximizes lazy spool rewinds because all duplicates are guaranteed to be encountered in a block. When outer input sort order is guaranteed, either by preserved ordering or an explicit Sort, the cost of the spool is much reduced. The optimizer factors in the impact of sort order on the number of spool rewinds and rebinds.
Plans with a Sort on the apply outer input, and a Lazy Table Spool on the inner input are quite common. The outer-side sorting optimization may still end up being counter-productive. For example, this can happen when the outer side cardinality estimate is so low that the sort ends up spilling to tempdb.
Apply lazy index spool
For an apply, getting a lazy index spool alternative depends on plan shape as well as costing.
The optimizer requires:
- Some duplicate join values on the outer input.
- An equality join predicate (or a logical equivalent the optimizer understands, such as
x <= y AND x >= y). - A guarantee that the outer references are unique below the proposed lazy index spool.
In execution plans, the required uniqueness is often provided by an aggregate grouping by the outer references, or a scalar aggregate (one with no group by). Uniqueness may also be provided in other ways, for example by the existence of a unique index or constraint.
A toy example that shows the plan shape is below:
CREATE TABLE #T1
(
c1 integer NOT NULL
);
GO
INSERT #T1 (c1)
VALUES
-- Duplicate outer rows
(1), (2), (3), (4), (5), (6),
(1), (2), (3), (4), (5), (6),
(1), (2), (3), (4), (5), (6);
GO
SELECT *
FROM #T1 AS T1
CROSS APPLY
(
SELECT COUNT_BIG(*)
FROM (SELECT T1.c1 UNION SELECT NULL) AS U
) AS CA (c);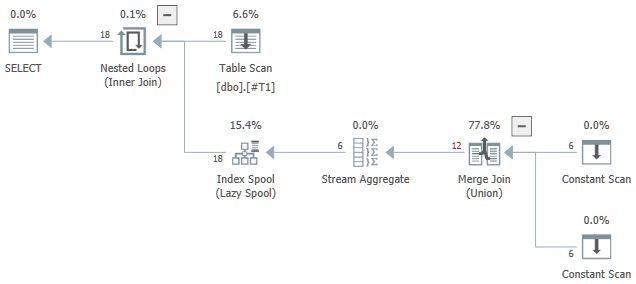
Notice the Stream Aggregate below the Lazy Index Spool.
If the plan shape requirements are met, the optimizer will often generate a lazy index alternative (subject to the caveats mentioned earlier). Whether the final plan includes a lazy index spool or not depends on costing.
Index versus table spool
The number of estimated rewinds and rebinds for a lazy index spool is the same as for a lazy table spool without sorted apply outer input.
This may seem like a rather unfortunate state of affairs. The primary advantage of an index spool is that it caches all previously seen results. This ought to make index spool rewinds more likely than for a table spool (without outer-input sorting) in the same circumstances. My understanding is that this quirk exists because without it, the optimizer would choose an index spool far too often.
Regardless, the cost model adjusts for the above to some extent by using different initial and subsequent-row I/O and CPU cost numbers for index and table spools. The net effect is that an index spool is usually costed lower than a table spool without sorted outer input, but remember the restrictive plan shape requirements, which make lazy index spools relatively rare.
Still, the primary cost competitor to a lazy spool index is a table spool with sorted outer input. The intuition for this is fairly straightforward: Sorted outer input means the table spool is guaranteed to see all duplicate outer references sequentially. This means it will rebind only once per distinct value, and rewind for all duplicates. This is the same as the expected behaviour of an index spool (logically speaking at least).
In practice, an index spool is more likely to be preferred over a sort-optimized table spool for fewer duplicate apply key values. Having fewer duplicate keys reduces the rewind advantage of the sort-optimized table spool, compared with the “unfortunate” index spool estimates noted previously.
The index spool option also benefits as the estimated cost of a table spool outer-side Sort increases. This would most often be associated with more (or wider) rows at that point in the plan.
Trace flags and hints
- Performance spools can be disabled with lightly-documented trace flag 8690, or the documented query hint
NO_PERFORMANCE_SPOOLin SQL Server 2016 or later. - Undocumented trace flag 8691 can be used (on a test system) to always add a performance spool when possible. The type of lazy spool you get (row count, table, or index) cannot be forced, it still depends on cost estimation.
- Undocumented trace flag 2363 can be used with the new cardinality estimation model to see the derivation of the distinct estimate on the outer input to an apply, and cardinality estimation in general.
- Undocumented trace flag 9198 can be used to disable lazy index performance spools specifically. You may still get a lazy table or row count spool instead (with or without sort optimization), depending on costing.
- Undocumented trace flag 2387 can be used to reduce the CPU cost of reading rows from a lazy index spool. This flag affects general CPU cost estimates for reading a range of rows from a b-tree. This flag tends to make index spool selection more likely, for cost reasons.
Other trace flags and methods to determine which optimizer rules were activated during query compilation can be found in my Query Optimizer Deep Dive series.
Final Thoughts
There are a great many internal details that affect whether the final execution plan uses a performance spool or not. I have tried to cover the main considerations in this article, without getting too far into the extremely intricate details of spool operator costing formulas. Hopefully there is enough general advice here to help you determine possible reasons for a particular performance spool type in an execution plan (or lack thereof).
Performance spools often get a bad rap, I think it is fair to say. Some of this is no doubt deserved. Many of you will have seen a demo where a plan executes faster without a “performance spool” than with. To some extent that is not unexpected. Edge cases exist, the costing model is not perfect, and no doubt demos often feature plans with poor cardinality estimates, or other optimizer-limiting issues.
That said, I do sometimes wish SQL Server would provide some sort of warning or other feedback when it resorts to adding a lazy table spool to a nested loops join (or an apply without a utilized supporting inner-side index). As mentioned in the main body, these are the situations I find most often going badly wrong, when cardinality estimates turn out to be horribly low.
Perhaps one day the query optimizer will factor in some concept of risk to plan choices, or provide more “adaptive” capabilities. In the meantime, it pays to support your nested loops joins with useful indexes, and to avoid writing queries that can only be implemented using nested loops where possible. I’m generalizing of course, but the optimizer tends to do better when it has more choices, a reasonable schema, good metadata, and manageable T-SQL statements to work with. As do I, come to think of it.
Other spool articles
Non-performance spools are used for many purposes within SQL Server, including:
- Halloween Protection
- Some row-mode window functions
- Computing multiple aggregates
- Optimizing statements that change data
Thanks for reading.
