Row Goals 4: An Anti Join Anti Pattern

Series links: Part 1 | Part 2 | Part 3 | Part 4 |

Apply Anti Join with a Top operator

You will often see an inner-side TOP (1) operator in apply anti join execution plans. For example, using the AdventureWorks database:

SELECT P.ProductID 
FROM Production.Product AS P
WHERE
    NOT EXISTS
    (
        SELECT 1
        FROM Production.TransactionHistory AS TH
        WHERE TH.ProductID = P.ProductID
    );

The plan shows a TOP (1) operator on the inner side of the apply (outer references) anti join:

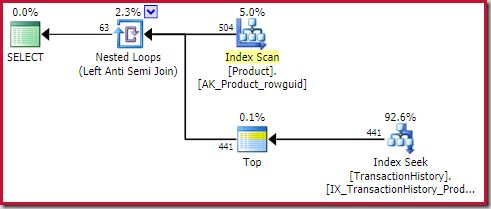
This Top operator is completely redundant. It is not required for correctness, efficiency, or to ensure a row goal is set.

The apply anti join operator will stop checking for rows on the inner side (for the current iteration) as soon as one row is seen at the join. It is perfectly possible to generate an apply anti join plan without the Top. So why is there a Top operator in this plan?

Source of the Top Operator

To understand where this pointless Top operator comes from, we need to follow the major steps taken during the compilation and optimization of our example query.

As usual, the query is first parsed into a tree. This features a logical ‘not exists’ operator with a subquery, which closely matches the written form of the query in this case:

The not exists subquery is unrolled into an apply anti join:

This is then further transformed into a logical left anti semi join. The resulting tree passed to cost-based optimization looks like this:

Logical distinct

The first exploration performed by the cost-based optimizer is to introduce a logical distinct operation on the lower anti join input, to produce unique values for the anti join key. The general idea is that instead of testing duplicated values at the join, the plan might benefit from grouping those values up front.

The responsible exploration rule is called LASJNtoLASJNonDist (left anti semi join to left anti semi join on distinct). No physical implementation or costing has been performed yet, so this is just the optimizer exploring a logical equivalence, based on the presence of duplicate ProductID values. The new tree with the grouping operation added is shown below:

Apply

The next logical transformation considered is to rewrite the join as an apply. This is explored using rule LASJNtoApply (left anti semi join to apply with relational selection). As mentioned earlier in the series, the earlier transformation from apply to join was to enable transformations that work specifically on joins. It is always possible to rewrite a join as an apply, so this expands the range of optimizations available.

Now, the optimizer does not always consider an apply rewrite as part of cost-based optimization. There has to be something in the logical tree to make it worthwhile pushing the join predicate down the inner side. Typically, this will be the existence of a matching index, but there are other promising targets. In this case, it is the logical key on ProductID created by the aggregate operation.

The result of this rule is a correlated anti join with selection on the inner side:

Selection pushdown

Next, the optimizer considers moving the relational selection (the correlated join predicate) further down the inner side, past the distinct (group by aggregate) introduced by the optimizer previously. This is done by rule SelOnGbAgg, which moves as much of a selection (predicate) past a suitable group by aggregate as it can (part of the selection may be left behind). This activity helps push selections as close to the leaf-level data access operators as possible, to eliminate rows earlier and make later index matching easier.

In this case, the filter is on the same column as the grouping operation, so the transformation is valid. It results in the whole selection being pushed under the aggregate:

Conversion to top

The final operation of interest is performed by rule GbAggToConstScanOrTop. This transform looks to replace a group by aggregate with a Constant Scan or Top logical operation. This rule matches our tree because the grouping column is constant for each row passing through the pushed-down selection. All rows are guaranteed to have the same ProductID. Grouping on that single value will always produce one row. Hence, it is valid to transform the aggregate to a Top (1). So this is where the top comes from.

Implementation and Costing

The optimizer now runs a series of implementation rules to find physical operators for each of the promising logical alternatives it has considered so far (stored efficiently in a memo structure). Hash and merge anti join physical options come from the initial tree with introduced aggregate (courtesy of rule LASJNtoLASJNonDist remember). The apply needs a little more work to build a physical top and match the selection to an index seek.

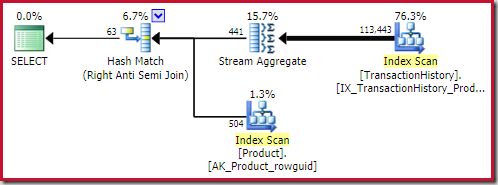
The best hash anti join solution found is costed at 0.362143 units:

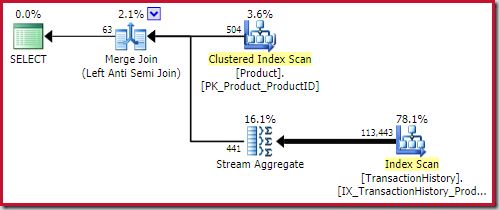
The best merge anti join solution comes in at 0.353479 units (slightly cheaper):

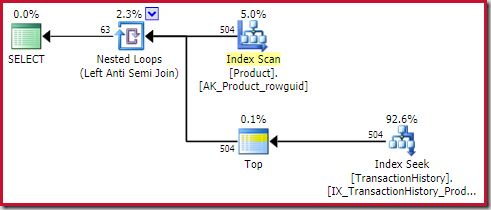
The apply anti join costs 0.091823 units (cheapest by a wide margin):

Cardinality

The astute reader may notice the row counts on the inner side of the apply anti join (504) differ from the previous screenshot of the same plan. This is because this is an estimated plan, while the previous plan was post-execution. When this plan is executed, only a total of 441 rows are found on the inner side over all iterations. This highlights one of the display difficulties with apply semi/anti join plans: The minimum optimizer estimate is one row, but a semi or anti join will always locate one row or no rows on each iteration. The 504 rows shown above represents 1 row on each of 504 iterations. To make the numbers match up, the estimate would need to be 441/504 = 0.875 rows each time, which would probably confuse people just as much.

Row goal

Anyway, the plan above is ‘lucky’ enough to qualify for a row goal on the inner side of the apply anti join for two reasons:

1. The anti join is transformed from a join to an apply in the cost-based optimizer. This sets a row goal (as established in part three).
2. The Top(1) operator also sets a row goal on its subtree.

The Top operator itself does not have a row goal (from the apply) since the row goal of 1 would not be less than the regular estimate, which is also 1 row (Card=1 for the PhyOp_Top below):

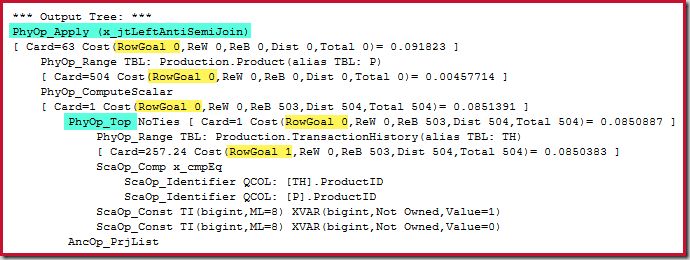
The Anti Join Anti Pattern

The following general plan shape is one I regard as an anti pattern:

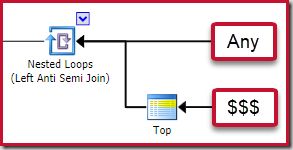
Not every execution plan containing an apply anti join with a Top (1) operator on its inner side will be problematic. Nevertheless, it is a pattern to recognise and one which almost always requires further investigation.

Plan shape

The four main elements to look out for are:

• A correlated nested loops (apply) anti join
• A Top (1) operator immediately on the inner side
• A significant number of rows on the outer input (so the inner side will be run many times)
• A potentially expensive subtree below the Top

The “$$$” subtree is one that is potentially expensive at runtime. This can be difficult to recognise. If we are lucky, there will be something obvious like a full table or index scan. In more challenging cases, the subtree will look perfectly innocent at first glance, but contain something costly when looked at more closely. To give a fairly common example, you might see an Index Seek that is expected to return a small number of rows, but which contains an expensive residual predicate that tests a very large number of rows to find the few that qualify.

The preceding AdventureWorks code example did not have a “potentially expensive” subtree. The Index Seek (without residual predicate) would be an optimal access method regardless of row goal considerations. This is an important point: providing the optimizer with an always-efficient data access path on the inner side of a correlated join is always a good idea. This is even more true when the apply is running in anti join mode with a Top (1) operator on the inner side.

Let’s look now at an example that has pretty dismal runtime performance due to this anti pattern.

Example

The following script creates two heap temporary tables. The first has 500 rows containing the integers from 1 to 500 inclusive. The second table has 500 copies of each row in the first table, for a total of 250,000 rows. Both tables use the sql_variant data type.

DROP TABLE IF EXISTS #T1, #T2;

CREATE TABLE #T1 (c1 sql_variant NOT NULL);
CREATE TABLE #T2 (c1 sql_variant NOT NULL);

-- Numbers 1 to 500 inclusive
-- Stored as sql_variant
INSERT #T1
    (c1)
SELECT
    CONVERT(sql_variant, SV.number)
FROM master.dbo.spt_values AS SV
WHERE 
    SV.[type] = N'P'
    AND SV.number >= 1
    AND SV.number <= 500;

-- 500 copies of each row in table #T1
INSERT #T2 
    (c1)
SELECT
    T1.c1
FROM #T1 AS T1
CROSS JOIN #T1 AS T2;

-- Ensure we have the best statistical information possible
CREATE STATISTICS sc1 ON #T1 (c1) WITH FULLSCAN, MAXDOP = 1;
CREATE STATISTICS sc1 ON #T2 (c1) WITH FULLSCAN, MAXDOP = 1;

Performance

We now run a query looking for rows in the smaller table that are not present in the larger table (of course there are none):

SELECT
    T1.c1 
FROM #T1 AS T1
WHERE 
    NOT EXISTS
    (
        SELECT 1
        FROM #T2 AS T2
        WHERE T2.c1 = T1.c1
    );

This query runs for about 20 seconds, which is awfully long time to compare 500 rows with 250,000. The SSMS estimated plan makes it hard to see why performance might be so poor:

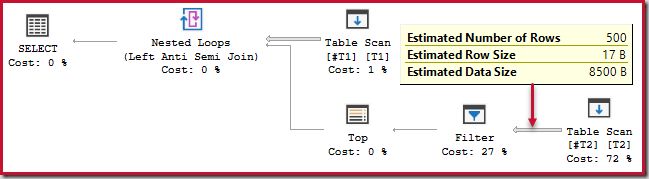
The observer needs to be aware that SSMS estimated plans show inner side estimates per iteration of the nested loop join. Confusingly, SSMS actual plans show the number of rows over all iterations. Plan Explorer automatically performs the simple calculations necessary for estimated plans to also show the total number of rows expected:

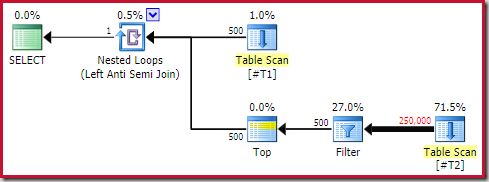
Even so, the runtime performance is much worse than estimated. The post-execution (actual) execution plan is:

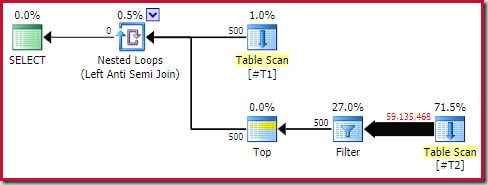
Note the separate Filter, which would normally be pushed down into the scan as a residual predicate. This is the reason for using the sql_variant data type; it prevents pushing the predicate, which makes the huge number of rows from the scan easier to see.

Analysis

The reason for the discrepancy comes down to how the optimizer estimates the number of rows it will need to read from the Table Scan to meet the one-row goal set at the Filter. The simple assumption is that values are uniformly distributed in the table, so to encounter 1 of the 500 unique values present, SQL Server will need to read 250,000 / 500 = 500 rows. Over 500 iterations, that comes to 250,000 rows.

The optimizer’s uniformity assumption is a general one, but it does not work well here. You can read more about this in A Row Goal Request by Joe Obbish, and vote for his suggestion on the Connect replacement feedback forum at Use More Than Density to Cost a Scan on the Inner Side of a Nested Loop with TOP.

My view on this specific aspect is that the optimizer should quickly back off from a simple uniformity assumption when the operator is on the inner side of a nested loops join (i.e. estimated rewinds plus rebinds is greater than one). It is one thing to assume that we need to read 500 rows to find a match on the first iteration of the loop. To assume this on every iteration seems awfully unlikely to be accurate; it means the first 500 rows encountered should contain one of each distinct value. This is highly unlikely to be the case in practice.

A Series of Unfortunate Events

Regardless of the way repeated Top operators are costed, it seems to me the whole situation should be avoided in the first place. Recall how the Top in this plan was created:

• The optimizer introduced an inner-side distinct aggregate as a performance optimization.
• This aggregate provides a key on the join column by definition (it produces uniqueness).
• This constructed key provides a target for the conversion from a join to an apply.
• The predicate (selection) associated with the apply is pushed down past the aggregate.
• The aggregate is now guaranteed to be operating on a single distinct value per iteration (since it is a correlation value).
• The aggregate is replaced by a Top (1).

All these transformations are valid individually. They are part of normal optimizer operations as it searches for a reasonable execution plan. Unfortunately, the outcome here is that the speculative aggregate introduced by the optimizer ends up being turned into a Top (1) with an associated row goal. The row goal leads to the inaccurate costing based on the uniformity assumption, and then to selection of a plan that is highly unlikely to perform well.

Now, one might object that the apply anti join would have a row goal anyway - without the above transformation sequence. The counterargument is that the optimizer would not consider transformation from anti join to apply anti join (setting the row goal) without the optimizer-introduced aggregate giving the LASJNtoApply rule something to bind to. In addition, we have seen (in part three) that if the anti join had entered cost-based optimization as an apply (instead of a join), there would again be no row goal.

In short, the row goal in the final plan is entirely artificial, and has no basis in the original query specification. The issue with the Top and row goal is a side-effect of this more fundamental aspect.

Workarounds

There are many potential solutions to this problem. Removing any one of the steps in the optimization sequence above will ensure the optimizer does not produce an apply anti join implementation with dramatically (and artificially) reduced costs. Hopefully this issue will be addressed in SQL Server sooner rather than later.

In the meantime, my advice is to watch out for the anti join anti pattern. Ensure the inner side of an apply anti join always has an efficient access path for all runtime conditions. If this is not possible, you may need to use hints, disable row goals, use a plan guide, or force a query store plan to get stable performance from anti join queries.

---

Series Summary

We have covered a lot of ground over the four installments, so here is a high level summary:

Part 1 – Setting and Identifying Row Goals

• Query syntax does not determine the presence or absence of a row goal.
• A row goal is only set when the goal is less than the regular estimate.
• Physical Top operators (including those introduced by the optimizer) add a row goal to their subtree.
• A FAST or SET ROWCOUNT statement sets a row goal at the root of the plan.
• Semi join and anti join may add a row goal.
• SQL Server 2017 CU3 adds the showplan attribute EstimateRowsWithoutRowGoal for operators affected by a row goal
• Row goal information can be revealed by undocumented trace flags 8607 and 8612.

Part 2 – Semi Joins

• It is not possible to express a semi join directly in T-SQL, so we use indirect syntax e.g. IN, EXISTS, or INTERSECT.
• These syntaxes are parsed into a tree containing an apply (correlated join).
• The optimizer attempts to transform the apply into a regular join (not always possible).
• Hash, merge, and regular nested loops semi join do not set a row goal.
• Apply semi join always sets a row goal.
• Apply semi join can be recognized by having Outer References on the nested loops join operator.
• Apply semi join does not use a Top (1) operator on the inner side.

Part 3 – Anti Joins

• Also parsed into an apply, with an attempt to rewrite that as a join (not always possible).
• Hash, merge, and regular nested loops anti join do not set a row goal.
• Apply anti join does not always set a row goal.
• Only cost-based optimization (CBO) rules that transform anti join to apply set a row goal.
• The anti join must enter CBO as a join (not apply). Otherwise the join to apply transform cannot occur.
• To enter CBO as a join, the pre-CBO rewrite from apply to join must have succeeded.
• CBO only explores rewriting an anti join to an apply in promising cases.
• Pre-CBO simplifications can be viewed with undocumented trace flag 8621.

Part 4 – Anti Join Anti Pattern

• The optimizer only sets a row goal for apply anti join where there is a promising reason to do so.
• Unfortunately, multiple interacting optimizer transforms add a Top (1) operator to the inner side of an apply anti join.
• The Top operator is redundant; it is not required for correctness or efficiency.
• The Top always sets a row goal (unlike the apply, which needs a good reason).
• The unwarranted row goal may lead to extremely poor performance.
• Watch out for a potentially expensive subtree under the artificial Top (1).

Thank you for reading.