Cardinality Estimation: Combining Density Statistics

Introduction

This article shows how SQL Server combines density information from multiple single-column statistics, to produce a cardinality estimate for an aggregation over multiple columns. The details are hopefully interesting in themselves. They also provide an insight into some of the general approaches and algorithms used by the cardinality estimator.

Consider the following AdventureWorks sample database query, which lists the number of product inventory items in each bin on each shelf in the warehouse:

SELECT 
    INV.Shelf, 
    INV.Bin, 
    COUNT_BIG(*)
FROM Production.ProductInventory AS INV
GROUP BY 
    INV.Shelf,
    INV.Bin
ORDER BY 
    INV.Shelf,
    INV.Bin;

The estimated execution plan shows 1,069 rows being read from the table, sorted into Shelf and Bin order, then aggregated using a Stream Aggregate operator:

Estimated Execution Plan

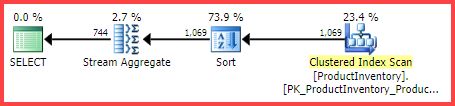
The question is, how did the SQL Server query optimizer arrive at the final estimate of 744 rows?

Available Statistics

When compiling the query above, the query optimizer will create single-column statistics on the Shelf and Bin columns, if suitable statistics do not already exist. Among other things, these statistics provide information about the number of distinct column values (in the density vector):

DBCC SHOW_STATISTICS 
(
    [Production.ProductInventory], 
    [Shelf]
)
WITH DENSITY_VECTOR;

DBCC SHOW_STATISTICS 
(
    [Production.ProductInventory], 
    [Bin]
)
WITH DENSITY_VECTOR;

The results are summarized in the table below (the third column is calculated from the density):

Column	Density	1/Density
Shelf	0.04761905	21
Bin	0.01612903	62

Shelf and Bin density vector information

As the documentation notes, the reciprocal of the density is the number of distinct values in the column. From the statistics information shown above, SQL Server knows that there were 21 distinct Shelf values and 62 distinct Bin values in the table, when the statistics were collected.

The task of estimating the number of rows produced by a GROUP BY clause is trivial when only a single column is involved (assuming no other predicates). For example, it is easy to see that GROUP BY Shelf will produce 21 rows; GROUP BY Bin will produce 62.

However, it is not immediately clear how SQL Server can estimate the number of distinct (Shelf, Bin) combinations for our GROUP BY Shelf, Bin query.

To put the question in a slightly different way: Given 21 shelves and 62 bins, how many unique shelf and bin combinations will there be?

Leaving aside physical aspects and other human knowledge of the problem domain, the answer could be anywhere from max(21, 62) = 62 to (21 * 62) = 1,302. Without more information, there is no obvious way to know where to pitch an estimate in that range.

Yet, for our example query, SQL Server estimates 744.312 rows (rounded to 744 in the Plan Explorer view) but on what basis?

Cardinality Estimation Extended Event

The documented way to look into the cardinality estimation process is to use the Extended Event query_optimizer_estimate_cardinality (despite it being in the “debug” channel).

While a session collecting this event is running, execution plan operators gain an additional property StatsCollectionId that links individual operator estimates to the calculations that produced them. For our example query, statistics collection id 2 is linked to the cardinality estimate for the group by aggregate operator.

The relevant output from the Extended Event for our test query is:

<data name="calculator">
    <type name="xml" package="package0"></type>
    <value>
    <calculatorlist>
        <distinctcountcalculator calculatorname="CDVCPlanLeaf" singlecolumnstat="Shelf,Bin">
    </distinctcountcalculator></calculatorlist>
    </value>
</data>
<data name="stats_collection">
    <type name="xml" package="package0"></type>
    <value>
    <statscollection name="CStCollGroupBy" id="2" card="744.31">
        <loadedstats>
        <statsinfo dbid="6" objectid="258099960" statsid="3">
        <statsinfo dbid="6" objectid="258099960" statsid="4">
        </statsinfo></statsinfo></loadedstats>
    </statscollection>
    </value>
</data>

There is some useful information there, for sure.

We can see that the plan leaf distinct values calculator class (CDVCPlanLeaf) was employed, using single column statistics on Shelf and Binas inputs. The stats collection element matches this fragment to the id (2) shown in the execution plan, which shows the cardinality estimate of 744.31, and more information about the statistics object ids used as well.

Unfortunately, there is nothing in the event output to say exactly how the calculator arrived at the final figure, which is the thing we are really interested in.

Combining distinct counts

Going a less documented route, we can request an estimated plan for the query with trace flags 2363 and 3604 enabled:

SELECT 
    INV.Shelf, 
    INV.Bin, 
    COUNT_BIG(*)
FROM Production.ProductInventory AS INV
GROUP BY 
    INV.Shelf,
    INV.Bin
ORDER BY 
    INV.Shelf,
    INV.Bin
OPTION (QUERYTRACEON 3604, QUERYTRACEON 2363);

This returns debug information to the Messages tab in SQL Server Management Studio. The interesting part is reproduced below:

Begin distinct values computation
Input tree:
  LogOp_GbAgg OUT(QCOL: [INV].Shelf,QCOL: [INV].Bin,COL: Expr1001 ,) BY(QCOL: [INV].Shelf,QCOL: [INV].Bin,)
      CStCollBaseTable(ID=1, CARD=1069 TBL: Production.ProductInventory AS TBL: INV)
      AncOp_PrjList 
          AncOp_PrjEl COL: Expr1001 
              ScaOp_AggFunc stopCountBig
                  ScaOp_Const TI(int,ML=4) XVAR(int,Not Owned,Value=0)

Plan for computation:
  CDVCPlanLeaf
      0 Multi-Column Stats, 2 Single-Column Stats, 0 Guesses

Loaded histogram for column QCOL: [INV].Shelf from stats with id 3
Loaded histogram for column QCOL: [INV].Bin from stats with id 4

Using ambient cardinality 1069 to combine distinct counts:
  21
  62

Combined distinct count: 744.312
Result of computation: 744.312

Stats collection generated: 
  CStCollGroupBy(ID=2, CARD=744.312)
      CStCollBaseTable(ID=1, CARD=1069 TBL: Production.ProductInventory AS TBL: INV)

End distinct values computation

This shows much the same information as the Extended Event did in an (arguably) easier to consume format:

• The input relational operator to compute a cardinality estimate for (LogOp_GbAgg– logical group by aggregate)
• The calculator used (CDVCPlanLeaf) and input statistics
• The resulting statistics collection details

The interesting new piece of information is the part about using ambient cardinality to combine distinct counts.
This clearly shows that the values 21, 62, and 1069 were used, but (frustratingly) still not exactly which calculations were performed to arrive at the 744.312 result.

To The Debugger!

Attaching a debugger and using public symbols allows us to explore in detail the code path followed while compiling the example query.
The snapshot below shows the upper portion of the call stack at a representative point in the process:

MSVCR120!log
sqllang!OdblNHlogN
sqllang!CCardUtilSQL12::ProbSampleWithoutReplacement
sqllang!CCardUtilSQL12::CardDistinctMunged
sqllang!CCardUtilSQL12::CardDistinctCombined
sqllang!CStCollAbstractLeaf::CardDistinctImpl
sqllang!IStatsCollection::CardDistinct
sqllang!CCardUtilSQL12::CardGroupByHelperCore
sqllang!CCardUtilSQL12::PstcollGroupByHelper
sqllang!CLogOp_GbAgg::PstcollDeriveCardinality
sqllang!CCardFrameworkSQL12::DeriveCardinalityProperties

There are a few interesting details here. Working from the bottom up, we see that cardinality is being derived using the updated CE (CCardFrameworkSQL12) available in SQL Server 2014 and later (the original CE is CCardFrameworkSQL7), for the group by aggregate logical operator (CLogOp_GbAgg).

Shannon entropy and mutual information

Computing the distinct cardinality involves combining (munging) multiple inputs, using sampling without replacement.

The reference to H and a (natural) logarithm in the second method from top shows the use of Shannon Entropy in the calculation:

Shannon Entropy

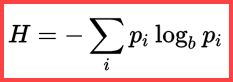
Entropy can be used to estimate the informational correlation (mutual information) between two statistics:

Mutual Information

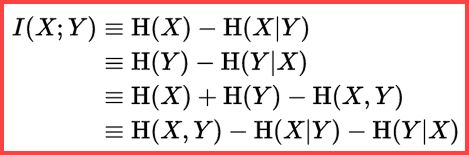
Calculation

Putting all this together, we can construct a T-SQL calculation script matching the way SQL Server uses sampling without replacement, Shannon Entropy, and mutual information to produce the final cardinality estimate.

We start with the input numbers (ambient cardinality and the number of distinct values in each column):

DECLARE 
    @Card float = 1069,
    @Distinct1 float = 21,
    @Distinct2 float = 62;

The frequency of each column is the average number of rows per distinct value:

DECLARE
    @Frequency1 float = @Card / @Distinct1,
    @Frequency2 float = @Card / @Distinct2;

Sampling without replacement (SWR) is a simple matter of subtracting the average number of rows per distinct value (frequency) from the total number of rows:

DECLARE
    @SWR1 float = @Card - @Frequency1,
    @SWR2 float = @Card - @Frequency2,
    @SWR3 float = @Card - @Frequency1 - @Frequency2;

Compute the entropies (N log N) and mutual information:

DECLARE
    @E1 float = (@SWR1 + 0.5) * LOG(@SWR1),
    @E2 float = (@SWR2 + 0.5) * LOG(@SWR2),
    @E3 float = (@SWR3 + 0.5) * LOG(@SWR3),
    @E4 float = (@Card + 0.5) * LOG(@Card);

-- Using logarithms allows us to express
-- multiplication as addition and division as subtraction
DECLARE
    @MI float = EXP(@E1 + @E2 - @E3 - @E4);

Now we have estimated how correlated the two sets of statistics are, we can compute the final estimate:

SELECT (1e0 - @MI) * @Distinct1 * @Distinct2;

The result of the calculation is 744.311823994677, which is 744.312 rounded to three decimal places.

Complete script

For convenience, here is the whole code in one block:

DECLARE 
    @Card float = 1069,
    @Distinct1 float = 21,
    @Distinct2 float = 62;

DECLARE
    @Frequency1 float = @Card / @Distinct1,
    @Frequency2 float = @Card / @Distinct2;

-- Sample without replacement
DECLARE
    @SWR1 float = @Card - @Frequency1,
    @SWR2 float = @Card - @Frequency2,
    @SWR3 float = @Card - @Frequency1 - @Frequency2;

-- Entropy
DECLARE
    @E1 float = (@SWR1 + 0.5) * LOG(@SWR1),
    @E2 float = (@SWR2 + 0.5) * LOG(@SWR2),
    @E3 float = (@SWR3 + 0.5) * LOG(@SWR3),
    @E4 float = (@Card + 0.5) * LOG(@Card);

-- Mutual information
DECLARE
    @MI float = EXP(@E1 + @E2 - @E3 - @E4);

-- Final estimate
SELECT (1e0 - @MI) * @Distinct1 * @Distinct2;

Final Thoughts

The final estimate is imperfect in this case—the example query actually returns 441 rows.

To obtain an improved estimate, we could provide the optimizer with better information about the density of the Bin and Shelf columns using a multicolumn statistic. For example:

CREATE STATISTICS stat_Shelf_Bin 
ON Production.ProductInventory (Shelf, Bin);

With that statistic in place (either as given, or as a side-effect of adding a similar multicolumn index), the cardinality estimate for the example query is exactly right. It is rare to compute such a simple aggregation though. With additional predicates, the multicolumn statistic may be less effective. Nevertheless, it is important to remember that the additional density information provided by multicolumn statistics can be useful for aggregations (as well as equality comparisons).

Without a multicolumn statistic, an aggregate query with additional predicates may still be able use the essential logic shown in this article. For example, instead of applying the formula to the table cardinality, it may be applied to input histograms step by step.

Related reading

• Cardinality Estimation for a Predicate on a COUNT Expression