Bitmap Magic

Question

Can a parallel query use less CPU than the same serial query, while executing faster?

The answer is yes! To demonstrate, I’ll use the following two (heap) tables, each containing a single column typed as integer:

Sample Data

Let’s load the #BuiltInt table with 5,000 random integer values (I’m using RAND with a seed and a WHILE loop so you will get the same random numbers if you run this script yourself):

Now load the #Probe table with 5,000,000 random integers:

Finding Matches - Serial Plan

Now let’s write a query to count the number of matches, using a MAXDOP 1 query hint to ensure that the execution plan uses only a single processor. The illustration below shows the query, execution plan, and runtime statistics:

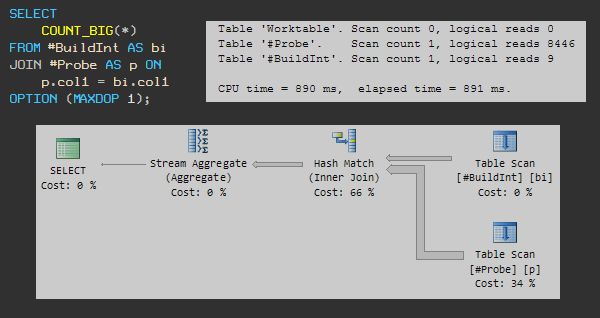
It turns out there are 13 matches. This query uses 890ms of CPU time and runs for 891ms.

Finding Matches - Parallel Plan

Now lets run the same query, but with a MAXDOP 2 hint:

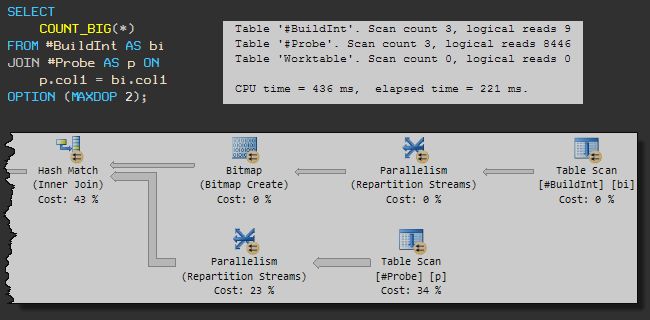
The query now completes in 221ms using 436ms of CPU time. That’s a 4x speed-up, while using half the CPU!

Bitmap Magic

The reason the parallel query is so much more efficient is down to the Bitmap operator.

To more clearly see the effect it has, take a look at the parallel execution plan with runtime statistics included (an ‘actual’ plan):

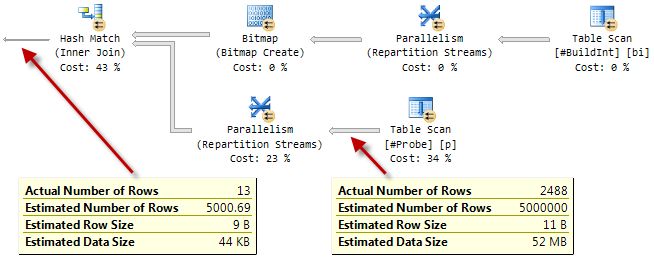
Compare that to the serial plan:

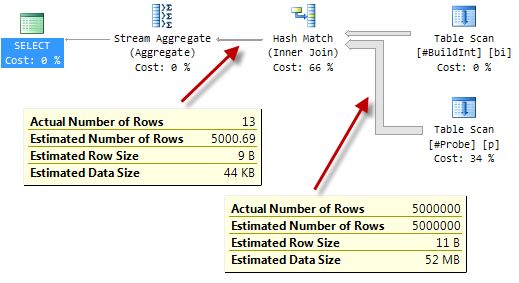
The way these bitmap filters work is reasonably well documented, so I’ll just give an outline here and provide links to some existing documentation at the end of this post.

Hash Join

A hash join proceeds in two phases.

1. It reads all the rows from its build input and constructs a hash table using the join keys.
2. It reads a row at a time from the probe input, uses the same hash function as before to compute a hash value for the probe row’s join keys, and uses this hash value to check a single hash table bucket for matches.

Naturally, the possibility of hash collisions means that the join generally still has to compare the real join key values to ensure a true match.

Bitmaps in Serial Plans

Most people don’t know that a hash match join always creates a bitmap, even in a serial plan. You can’t see the bitmap in the serial plan, because it is part of the internal implementation of the Hash Match iterator.

While processing build rows and creating its hash table, the hash join also sets one (or more) bits in a compact bitmap structure. When the build phase is complete, this bitmap provides an efficient way to check for potential hash matches without the cost of probing the hash table.

In the case of a serial-plan hash match, incoming probe rows to the hash join are hashed on the join keys and the value is used to check the bitmap. If the corresponding bits in the bitmap are all set, there might be a match in the hash table, so the process goes on to check the hash table.

Conversely, if even one of the bits corresponding to the hashed join key value is not set, we can be certain that there is no match in the hash table, and we can discard the current probe row immediately.

The relatively small cost of building the bitmap is offset by the time saved not checking rows that cannot match in the hash table. Since checking a bitmap is very much faster than probing a hash table, this optimization is often an effective one.

Bitmaps in Parallel Plans

In a parallel plan, a bitmap is exposed as a separate plan operator.

When the hash join transitions from its build phase to the probe phase, the bitmap is passed to an iterator on the probe side of the hash join. At minimum, the bitmap is pushed down the probe side as far as the exchange (Parallelism) operator immediately below the join.

At this location, the bitmap is able to eliminate rows that cannot join before the rows are passed between threads inside the exchange. There are no exchange operators in serial plans, of course, so moving the bitmap just outside the hash join in this way would confer no extra advantage compared to the ‘built in’ bitmap inside the hash match iterator.

In certain circumstances (though only in a parallel plan!) the query processor can push the bitmap even further down the plan on the probe side of the join. The idea here is that eliminating rows earlier saves the cost of moving rows between iterators unnecessarily, and perhaps even eliminates some operations completely.

As an aside, the optimizer generally tries to push ordinary filters toward the leaves of a plan for similar reasons—eliminating rows as early as possible is usually worthwhile.

I should mention though, that the type of bitmap we are dealing with here is added after optimization has completed. Whether this (static) type of bitmap is added to a post-optimizer plan or not is a decision made based on the expected selectivity of the filter (so accurate statistics are essential).

Pushing the Bitmap Filter

Back to the concept of pushing the bitmap filter further down the probe side of the join than the exchange iterator immediately below it.

In many cases, the bitmap filter can be pushed all the way down to a scan or seek. When this happens, the bitmap filter check appears as a residual predicate like this:

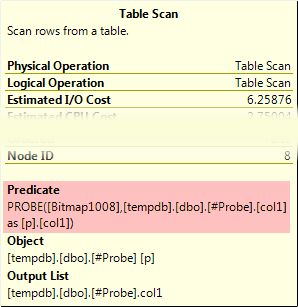
As a residual, it is applied to all rows that pass any seek predicates (for an index seek), or to all rows in the case of an index or table scan. The screenshot above shows a bitmap filter being applied to a heap table scan, for example.

Deeper Still…

If the bitmap filter is built on a single column or expression of the integer or bigint types, and if the bitmap is to be applied to a single column of integer or bigint type, it might be pushed down the plan even further than the seek or scan operator. The predicate is still shown in the seek or scan as above, but it is annotated with the INROW attribute, meaning the filter is pushed into the Storage Engine, and applied to rows as they are being read.

When this optimization occurs, rows are eliminated before the query processor sees the row at all. Only rows that might match the hash match join are passed up from the Storage Engine.

The exact circumstances in which this optimization is applied varies a little between SQL Server releases. For example, in SQL Server 2005, the probed column has to be defined as NOT NULL, in addition to the conditions noted previously. This restriction was relaxed in SQL Server 2008.

You might be wondering how much difference the INROW optimization makes. Surely pushing the filter as far down as the seek or scan must be nearly as good as pushing the filter into the Storage Engine? I’ll cover that interesting question in a future post. For now, I want to round off this entry by showing how merge join and nested loops join compare for this query.

Other Join Options

With no indexes, a query using the nested loops physical join type is an complete non-starter. We would have to scan one table fully for each row in the other table—a total of 5 billion comparisons. That query would likely run for a very long time.

Merge Join

This type of physical join requires sorted inputs, so forcing a merge join results in a plan that fully sorts both inputs before joining. The serial plan looks like this:

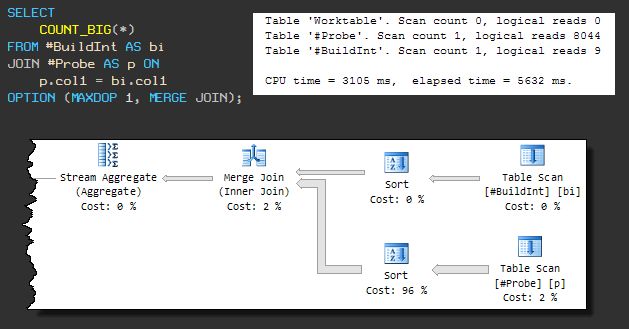
The query now uses 3105ms of CPU and overall execution time is 5632ms.

The extra non-CPU time there is due to one of the sort operations spilling to tempdb (despite SQL Server having more than sufficient memory available for the sort).

The spill occurs because the default memory grant algorithm happens to not reserve enough memory in advance. Leaving that to one side, it is clear that the query would never complete in less than 3105ms anyway, so we will move on.

Continuing to force a merge join plan, but allowing parallelism (MAXDOP 2) as before:

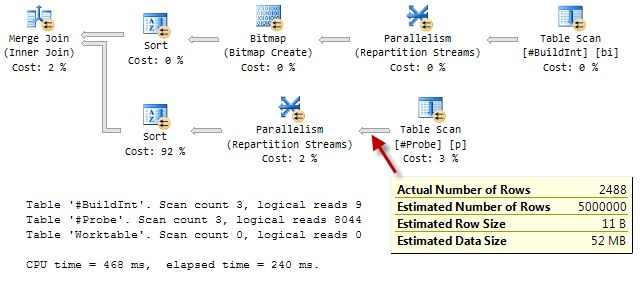
As in the parallel hash join plan seen earlier, the Bitmap filter is pushed down the other side of the merge join, all the way to the Table Scan, and applied using the INROW optimization.

At 468ms of CPU and 240ms elapsed time, the merge plan with the extra sorts is very nearly as fast as the parallel hash (436 ms/221 ms).

There is one downside to the parallel merge join plan: It reserves 330KB of workspace memory, based on the expected number of rows to sort. Since this type of bitmap is considered after cost-based optimization is complete, no adjustment is made to the estimate even though only 2488 rows flow through the lower sort.

A bitmap can only appear in a merge join plan if the bitmap is followed by a blocking operator (like a sort). A blocking operator has to consume its entire input before producing its first row, guaranteeing that the bitmap is fully populated before rows from the inner input start being read from the inner-side table and checked against the bitmap.

It is not necessary to have a blocking operator on the other side of the merge join, and neither does it matter which side the bitmap appears on.

With Indexes

The situation is different if suitable indexes are available. The distribution of the ‘random’ data is such that we can create a unique index on the build table, but the probe table contains duplicates so we have to make do with a non-unique index:

The hash join (both serial and parallel versions) is largely unaffected by the change. It cannot take advantage of the indexes, so the plans and performance are the same as seen previously.

Merge Join

The merge join no longer has to perform a many-to-many join operation, and also no longer requires a sort on either input.

The lack of a blocking sort operator means that the bitmap can no longer be used (and remember the optimizer has no say in the decision, so it rejects a sorting plan early on as being a silly idea).

The effect is that a serial plan is produced whatever setting for MAXDOP is specified, and performance is worse than the parallel plan before the indexes were added: 702ms CPU and 704ms elapsed time:

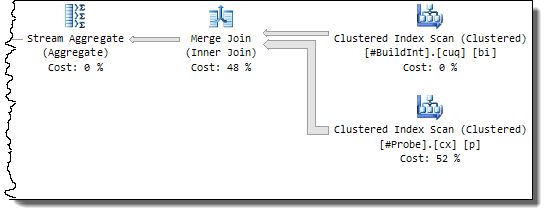
This does represent a marked improvement over the original serial merge join plan, however (3105ms/5632ms). This is due to the elimination of the sorts and the better performance of the one-to-many join.

Nested Loops Join

The nested loops join benefits enormously, as you would expect. As for merge join, the optimizer does not consider a parallel plan:

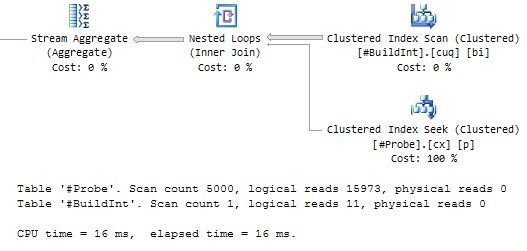
This is by far the best-performing query plan so far—just 16ms of CPU and 16ms elapsed time.

Of course, this assumes that the data required to satisfy the query is already in memory. Each seek into the probe table would otherwise generate essentially random I/O, so if you still store your data on a spinning magnetic film, cold-cache performance might be considerably worse.

On my laptop, a cold-cache nested loops run resulted in 78ms of CPU and 2152ms elapsed time. Under the same circumstances, the merge join plan used 686ms CPU and 1471ms elapsed; the hash join plan used 391ms CPU and 905ms elapsed.

Merge join and hash join both benefit from the larger, possibly sequential I/O issued by the read-ahead mechanism.

Further reading:

• Parallel Hash Join by Craig Freedman
• Query Execution Bitmap Filters by the SQL Server Query Processing Team
• Bitmaps in Microsoft SQL Server 2000 – MSDN Technical Article
• Interpreting Execution Plans Containing Bitmap Filters in Books Online
• Understanding Hash Joins in Books Online

---

Complete test script

USE tempdb;
GO
CREATE TABLE #BuildInt
(
    col1    INTEGER NOT NULL
);
GO
CREATE TABLE #Probe
(
    col1    INTEGER NOT NULL
);
GO
CREATE TABLE #ProbeDec
(
    col1    DECIMAL(10) NOT NULL
);
GO
-- Load 5,000 rows into the build table
SET NOCOUNT ON;
SET STATISTICS XML OFF;

DECLARE @I INTEGER = 1;

INSERT #BuildInt
    (col1) 
VALUES 
    (CONVERT(INTEGER, RAND(1) * 2147483647));

WHILE @I < 5000
BEGIN
    INSERT #BuildInt
        (col1)
    VALUES 
        (RAND() * 2147483647);
    SET @I += 1;
END;

INSERT #BuildDec
    (col1)
SELECT 
    CONVERT(DECIMAL(10), bi.col1)
FROM #BuildInt AS bi;
GO
-- Load 5,000,000 rows into the probe table
SET NOCOUNT ON;
SET STATISTICS XML OFF;

DECLARE @I INTEGER = 1;

INSERT #Probe
    (col1) 
VALUES 
    (CONVERT(INTEGER, RAND(2) * 2147483647));

BEGIN TRANSACTION;
WHILE @I < 5000000
BEGIN
    INSERT #Probe
        (col1) 
    VALUES 
        (CONVERT(INTEGER, RAND() * 2147483647));

    SET @I += 1;

    IF @I % 25 = 0
    BEGIN
        COMMIT TRANSACTION;
        BEGIN TRANSACTION;
    END;
END;

COMMIT TRANSACTION;
GO
-- Demos
SET STATISTICS XML OFF;
SET STATISTICS IO, TIME ON;

-- Serial
SELECT 
    COUNT_BIG(*) 
FROM #BuildInt AS bi 
JOIN #Probe AS p ON 
    p.col1 = bi.col1 
OPTION (MAXDOP 1);

-- Parallel
SELECT 
    COUNT_BIG(*) 
FROM #BuildInt AS bi 
JOIN #Probe AS p ON 
    p.col1 = bi.col1 
OPTION (MAXDOP 2);

SET STATISTICS IO, TIME OFF;

-- Indexes
CREATE UNIQUE CLUSTERED INDEX cuq ON #BuildInt (col1);
CREATE CLUSTERED INDEX cx ON #Probe (col1);

-- Vary the query hints to explore plan shapes

SELECT 
    COUNT_BIG(*) 
FROM #BuildInt AS bi 
JOIN #Probe AS p ON 
    p.col1 = bi.col1 
OPTION (MAXDOP 1, MERGE JOIN);
GO
DROP TABLE #BuildInt, #Probe;