Inside the Optimizer: Row Goals In Depth

Background

One of the core assumptions made by the SQL Server query optimizer cost model is that clients will eventually consume all the rows produced by a query. This results in plans that favour the overall execution cost, though it may take longer to begin producing rows.

Let’s look at an AdventureWorks example:

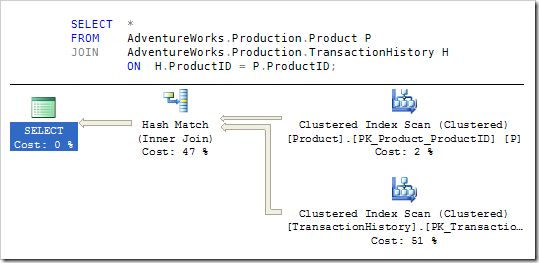
The optimizer chooses to perform the logical join using a Hash Match physical iterator, resulting in a plan with a total estimated cost of around 1.4 units.

By forcing alternative physical joins using a query hint, we see that a plan based on a merge join would have an estimated cost of just under 10, and a nested loops join would cost over 18 units.

All these cost estimates are based on the assumption that all rows are required.

Hash match

As detailed in Iterators, Query Plans, and Why They Run Backwards, the Hash Match iterator starts by consuming all rows produced by its build input (the Product table) in order to build a hash table. This makes Hash Match a semi-blocking iterator. It can only start producing output rows once the build phase is complete. If we need only the first few rows from the query quickly, this join type may not be the optimal choice.

Merge join

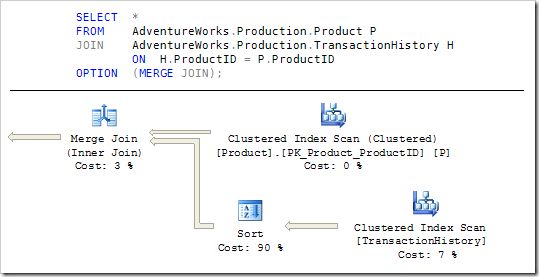
How quickly a merge join starts producing rows depends on whether any of its inputs need to be explicitly sorted. If the merge can acquire ordered rows on both inputs from an index or a prior operation without sorting, it can stream rows to its parent without a start-up delay.

The Sort query plan iterator is always a blocking operation, since we can’t know which row will sort first without examining them all. In the example query, the rows from the history table do need to be explicitly sorted, so a merge join would not be a good plan choice to get the first rows quickly:

Nested loops

Our third join option is Nested Loops, which is a generally a pipelined iterator. This means no start-up delay, and the first matching rows are returned quickly. Unfortunately, it also has the highest per-row estimated cost of the three physical join options.

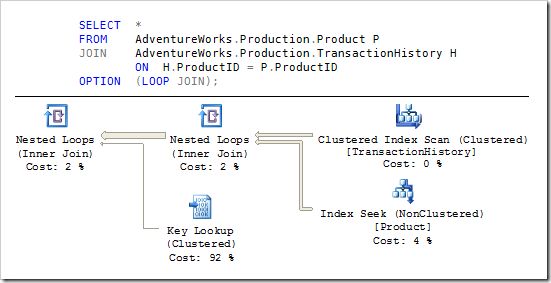
The Nested Loops iterator executes its inner (lower) input once for every row produced by its outer (top) input, making its overall cost proportional to the product of the number rows on its child inputs. By contrast, the hash and merge join strategies scan each of their inputs once, resulting in a cost which is proportional to the sum of the input rows.

The TOP Clause

Returning the first few rows produced by a query is a problem easily solved from the query-writer’s perspective: just add a TOP clause.

Imagine that we are just interested in seeing one row of output from our example query:

SELECT TOP (1) *
FROM Production.TransactionHistory AS H
JOIN Production.Product AS P
    ON  H.ProductID = P.ProductID;

The original query returns 113,443 rows. This query returns just one, and does so very quickly. So far so very obvious you might be thinking—but all is not what it seems.

A brief digression concerning TOP and deterministic results

I should mention that the TOP (1) query above contains a ‘bug’: There is no ORDER BY clause to determine which row qualifies as ‘top’.

In principle, the row produced by that query could be selected at random. In practice, the results depend on the query plan and internal implementation details in SQL Server. Since either of those things could change at any time, you should almost always specify a fully deterministic ORDER BY clause when using TOP.

If you’re wondering what might be non-deterministic about an ORDER BY clause, consider what might happen if we added ORDER BY P.ProductID to the query. A difficulty arises since ProductID is not unique for each row of the result set — the transaction history table may contain many rows for each product.

As a concrete example, assume that product #1 is the lowest ProductID, and there are 75 history records for that product. These 75 records all sort equally on ProductID, so which record will be returned by a TOP (1) operation? Who knows.

There are two ways to make the operation deterministic:

1. We could rewrite the ORDER BY clause to include a combination of columns that form a unique key over the output rows. Adding Transaction ID from the history table would achieve that here.
2. We could add WITH TIES to the TOP specification, though this would produce more than one row in case of duplicates.

I have omitted the ORDER BY on the example query because I truly do not mind which row we get and I need to avoid changing the semantic of the original query to demonstrate a point.

The TOP (1) plan

The TOP (1) query plan looks like this:

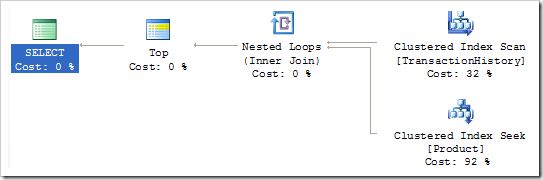
That looks very different from the original query plan, which featured a hash join. Clearly, when we add a TOP clause to a query, the optimizer does much more than just add a TOP iterator to the root of the plan it would have produced normally.

For comparison purposes, here is a query plan produced for the TOP (1) query when a hash join is forced:

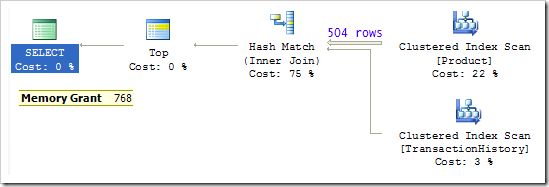
The important thing to notice is that the build input to the hash join must consume all 504 rows from the Product table before it can start probing the hash table for matches using rows from the TransactionHistory table.

Like all hashing operations, the hash join also requires a memory grant before the plan can start executing. The estimated cost of the hash join plan above is 0.1, while the nested loops join plan selected by the optimizer has an estimated cost of 0.01 units.

Row Goals

The challenges involved in producing an optimized query plan for row-limited queries—while retaining good general optimization performance for full-result queries—are more complex than simply replacing hash or merge join iterators with nested loops.

It would be reasonably straightforward to cater for queries with a TOP at the root of a plan, using specific code designed to recognise specific scenarios. However, that approach would miss wider opportunities for plan optimization in more general cases.

The TOP clause can be specified multiple times, in multiple places in a query declaration:

• At the outermost scope (as in the example)
• In a sub-query
• In a common table expression

Any of the above may be arbitrarily complex. The FAST n query hint can also be used to ask the optimizer to prefer a plan which will produce the first n rows quickly, while not restricting the total number of rows returned overall, as is the case with TOP.

As a final example, consider that a logical semi-join (such as a subquery introduced with EXISTS) shares the overall theme; it should also be optimized to find the first matching row quickly.

The SQL Server query optimizer provides a way to meet all these requirements by introducing the concept of a row goal. This establishes a target number of rows to ‘aim for’ at a particular point in the plan.

Framework

The optimizer changes required to enable the row goal feature are largely self-contained, sitting in a thin layer on top of the normal optimization activities.

This functional separation from common components (such as the costing engine and cardinality estimation) reduces the risk of breaking changes, minimises development effort, and simplifies testing.

The design also allows the optimizer to re-use existing facilities to explore the space of possible plans without special handling for regions constrained by a row goal.

The plan choices for the subtree below the row goal are generated using the common exploration rules used for full-result queries. For example, optimization of our simple query will consider all three physical join implementations, different access paths to the physical tables (indexes), and alternative orders for the join inputs.

Costing and cardinality

An important difference arises when the optimizer comes to decide which candidate plan is ‘best’. The normal routines produce iterator costs and cardinality estimates based on the query running to completion. In our example query, this results in a plan using a hash join, with the Product table chosen as the build input.

Normal cardinality & selectivity estimation starts at the plan leaves (an Index Scan, for example) and works up the plan modifying the statistics (frequencies and histograms) and cardinality estimates as it encounters iterators.

Some iterators (like Filter) have a simple effect on statistics and cardinalities, whereas others (joins, unions) may require more complex calculations and histogram adjustments.

When a row goal is present, the optimizer subsequently works down the plan (from the row goal toward the plan leaves) modifying iterator costs and cardinality estimates to reflect that goal.

To explain, let’s run our test query again, but this time specifying TOP (50):

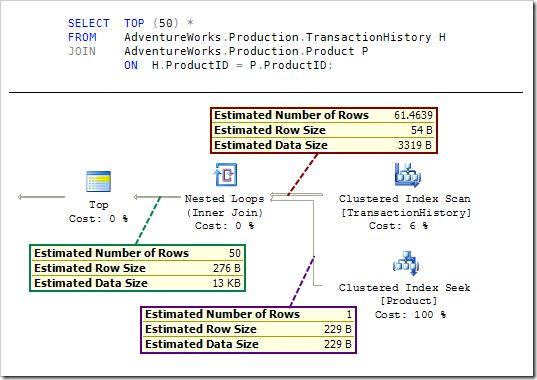
Working down the plan from the Top iterator, notice that the cardinality estimate is 50, as required by the row goal.

The estimate for the number of rows from each execution of the Index Seek is 1 (since the Product ID column is a key).

The estimated cardinality of the other join input is more interesting and requires a little more explanation…

Reverse cardinality estimation

Here is one more query to show the same query plan but without a row goal:

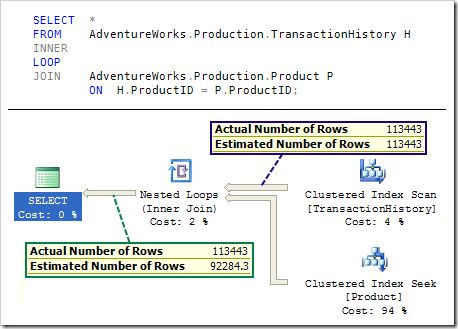
Regular cardinality estimation (without a row goal) determines that the 113,443 TransactionHistory rows, when joined to the Product table, should produce 92,284.3 rows. Leaving aside the fact that this calculation is wrong (and ignores the PK-FK relationship between the two tables), we can see that 113,443 / 92,284.3 = 1.22928 (using floating-point arithmetic).

That factor is used in the row goal calculation when working back past the nested loops join iterator. The output cardinality is 50 (the row goal) so the outer input to the loop join is estimated to produce 50 * 1.22928 = 61.46400 rows. That matches the estimated number of rows in the row goal plan, and illustrates the working-backwards nature of row goal cardinality estimation.

It is possible for cardinality estimation errors to produce a new estimate which is greater than the total number of rows in the source. This condition is detected, and cardinality estimations are capped to the known maximum row count if necessary.

Interesting side effects

A similar calculation applies to the inner side of the loops join, but it is reported slightly differently. In the plan with a row-goal, the inner input cardinality is estimated to be 1, but the estimated number of executions is a row-goal modified value:

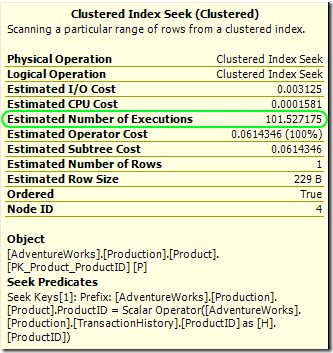
Notice also that the estimated I/O and CPU costs for the operator are not scaled; they show the per-execution cost as if a row goal were not in effect.

The estimated operator cost is scaled to reflect the row goal; that value is used in the sub-tree cost calculations. The differences are easier to see on the outer input:

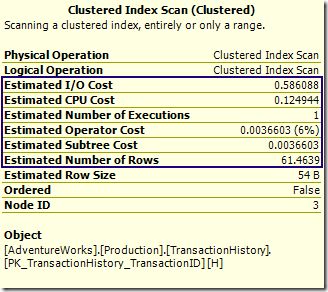
The Estimated I/O and CPU costs reflect the cost of returning all rows. The estimated ‘operator’ and ‘sub-tree’ costs are modified by the row goal.This feature of row goal plans often causes confusion, but next time someone asks you how the operator cost can be so much lower than its two components, you’ll have the answer!

The operator and sub-tree costs are used to determine which of the candidate plans is ‘best’. By performing these simple modifications, the row goal feature ensures that a plan is produced which reflects the row goal requirement.

Final Thoughts

Faced with seemingly contradictory requirements to optimize for full-query execution and early termination based on a specified row goal, the SQL Server query optimization team have produced an elegant solution.

Queries which use a row goal (TOP, FAST n, EXISTS and so on) benefit from all the transformation and optimizing tricks at SQL Server’s disposal, while still producing a cost-based plan.

To illustrate that last point, our test query chooses a loops join up to TOP (97). When TOP (98) is specified, the optimizer chooses a hash join on cost grounds. (The exact tipping point may be different on different versions of the product, and is dependent on statistics).

Hopefully this post has provided interesting insights into the internal workings of this very useful feature. Thanks for reading.